Séquence 1 - Algorithmes
![]()
La chaîne des opérations nécessaires à la résolution automatique de problèmes est la suivante :
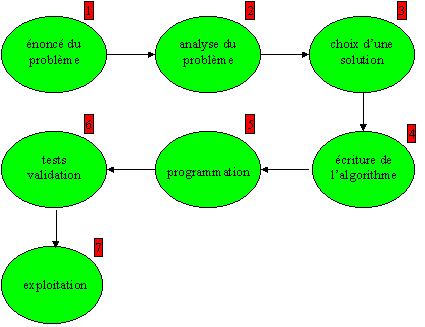
On ne s’intéressera ici qu’aux phases 1 à 5 et plus précisément aux phases 4 (algorithmique) et 5 (programmation).
Un algorithme est la description détaillée des opérations à effectuer pour résoudre un problème. Examinons tout d’abord quelques algorithmes dont les détails seront donnés ci-après :
exemple 1 : calcul de la somme de deux nombres : x, y --------> x+y
Le problème est simple ; l’algorithme correspondant est :
fonction somme(x,y) début somme = x+y ; fin |
L'écriture de l'algorithme utilise un langage spécial appelé langage algorithmique. Il s'agit d'un langage possédant des règles syntaxiques qui le rend proche d'un langage de programmation ; en fait le passage du langage algorithmique à un langage de programmation n'est souvent qu'une simple traduction.
L'algorithme consiste ici en un seul module dont le nom est "fonction somme(x,y)". Le corps du module est délimité par les mots "début" et "fin" et consiste ici en une seule instruction : somme = x+y ; . On notera qu'une instruction se termine par un ";". Ce module est du type fonction car ce module restitue une valeur (et une seule), la somme de x et de y qui figurent ici en paramètres d'entrée. Le résultat s'appelle somme, du nom de la fonction. Le signe "=" employé dans l'unique instruction n'est pas, contrairement à ce que l'on peut penser, le signe d'égalité mathématique, mais représente une affectation : la valeur x+y est affectée à la variable somme.
Ainsi, dans l'instruction "x = 3 ; ", la valeur 3 est affectée à la variable x. De même dans l'instruction "y = 2x - 1 ;", la variable y reçoit le double de la valeur de x diminué de 1. Enfin, dans l'instruction "z = z + 1 ;", la nouvelle valeur de la variable z est obtenue en augmentant de 1 l'ancienne valeur de z. On voit clairement sur cet exemple la différence entre l'égalité et l'affectation.
exemple 2 : calcul de factorielle n : n! = 1.2.3.4......n (avec par convention 0! = 1) . On veut donc, à partir de n, obtenir n!. Il y a plusieurs façons de procéder. L’algorithme ci-dessous décrit une solution :
fonction facto1(n)
début
facto1 = 1 ;
Si (n>0) alors
Pour i=2 à n faire
facto1 = facto1* i ;
FinPour
FinSi
fin
|
Comme on le verra ci-dessous, il existe d'autres façons de calculer la factorielle d'un nombre. Il existe en général, en effet, plusieurs algorithmes pour résoudre le même problème. Le module est ici plus important que celui de l'exemple 1. Il contient des structures conditionnelles et itératives que nous expliciterons plus loin. Comme dans le cas de l'exemple 1, ce module est une fonction qui fournit un résultat : la factorielle de n (qui est un paramètre d'entrée). On notera, dans l'instruction "facto1 = facto1*i ;"que la nouvelle valeur de facto1 est obtenue en multipliant l'ancienne valeur de facto1 par la valeur de i.
exemple 3 : calcul de la somme de n nombres. Soit un tableau de n nombres :
x[1], x[2], x[3],........, x[n]
On désire obtenir la somme x[1] + x[2] + x[3] +........+ x[n]
L’algorithme correspondant peut s’écrire :
fonction somtab(x[ ], n)
début
somtab = 0 ;
Pour i = 1 à n faire
somtab = somtab + x[i] ;
FinPour
fin
|
On retrouve ici encore une fonction dont le corps contient une structure itérative.
![]()
Exercices
1 - Ecrire un algorithme donnant la moyenne de trois nombres.
2 - Ecrire un algorithme de résolution de l'équation du premier degré ax+b = 0
3 - Etant donné un tableau de nombres, déterminer quel est le plus petit. (On s'inspirera de l'exemple 3).
4 - Que fait l'algorithme suivant ?
| fonction tagada (tsointsoin[
], n) début tagada = 0 Pour i = 1 à n faire tagada = tagada + tsointsoin*tsointsoin FinPour fin |
![]()
Solution des exercices
1 - Voici une proposition d'algorithme
| moyenne(a,b,c) début moyenne = (a+b+c)/3 fin |
2 - Equation du premier degré ax+b =0
| solution (a, b) début Si a = 0 alors Si b = 0 alors solution = "indétermination" Sinon solution = "impossiblité" FinSi Sinon solution = -b/a FinSi fin |
3 - Plus petit nombre d'un tableau de nombres
| Minimum(tab[ ],n) début Minimum = tab[1] Pour i = 1 à n faire Si tab[i] < Minimum alors Minimum = tab[i] FinSi FinPour fin |
4 - Cet algorithme décrit la manière d'obtenir la somme des carrés des nombres du tableau.